回答
下の図が答えだ。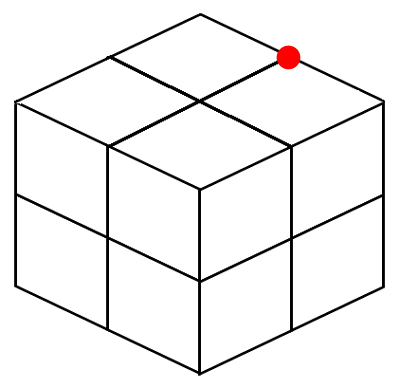
出題場所:記念館1階(グリンコにハーブティー)
立方体の同じ石が八個、図のように積んである。
PからAまでの長さを1とすると、PからBまでは2の長さである。
では、Pから3の長さになるのは図のどの点だろうか。
正しい点のひとつを囲んで答えよう。
もちろん直線距離で測ってほしい。
直角三角形の直角をなす2辺のそれぞれを二乗して足したものは、もう1辺(斜辺)の二乗と等しい。
ピタゴラッスの定理である。
ヒント1で、いきなりかたいことを書いてしまったが、定理を使って考えよう。
定理にあてはまるような直角三角形はないだろうか?
2辺の二乗を足したものが、3の二乗、つまり9に等しくなる三角形を見つけよう。
辺の長さが1と2の場所はすぐに見つかる。
この2辺が直角をなす場合、斜辺の長さは、2の二乗の4と1の二乗の1を足した5の平方根である。
つまりルート5だ。
下の図が答えだ。